Octavo problema de Apolonio

Este problema consiste en hallar las circunferencias tangentes a otras dos dadas y a una recta, también dada. El problema tiene ocho soluciones, por lo que vemos que se complica algo más que el resto de casos, pero este, como vamos a ver, se soluciona reduciéndolo al caso de un punto, una recta y una circunferencia.

El punto con el que trabajaremos es el centro de una de las circunferencias, la nueva circunferencia, será de radio, la suma de los radios, por lo tanto lo que hemos hecho es dilatar una de las circunferencias en la misma medida en que hemos reducido la otra. Lo mismo para la recta, que la consideramos una circunferencia de radio infinito.

Considerando los radios de las circunferencias R y r, respectivamente:Estas cuatro circunferencias se han obtenido considerando una circunferencia concéntrica de radio R+r; de las cuatro circunferencias, dos se obtienen con una de las paralelas y las otras dos con la otra.

Estas cuatro circunferencias solución se obtienen considerando ahora una circunferencia concéntrica de radio R-r y de nuevo, dos con una de las paralelas y otras dos con la otra.

Con esto, ya tenemos las ocho soluciones posibles al problema de hallar las circunferencias tangentes a otras 2 y a una recta.

Séptimo problema de Apolonio

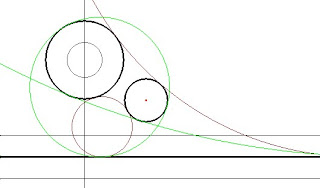
En este caso se intenta trazar una circunferencia que sea tangente a dos rectas y a otra circunferencia dadas.
Para resolver este problema lo que debemos hacer es trazar dos paralelas a una de las rectas a la distancia del radio de la circunferencia dada.A continuación hallamos el centro O' que es simétrico del centro O respecto a la bisectriz entre las dos rectas enunciado.La recta que pasa tanto por O y O' corta en N y M a las paralelas que hemos trazado antes.Realizamos una circunferencia auxiliar con centro en esa recta(la de O y O') y que pase por O y O',y hallamos los puntos de tangencia de la circunferencia desde M y N (en el dibujo sólo está hecho desde M). Nos llevamos la distancia del punto tangencial a la recta paralela que contiene al punto desde el cual hemos hallado las tangencias y trazamos una perpendicular.La intersección de esta perpendicular con la bisectriz entre las dos rectas enunciado será un centro solución.Podremos encontrar 4 soluciones.

Puede darse el caso de que la circunferencia sea tangente a una de las rectas,en cuyo caso el problema se haría igual,en el caso de la paralela exterior , y con la paralela interior se reduciría al caso de dos rectas y un punto.